The gossip property in Tendermint

Summary: I describe why the Tendermint algorithm requires the gossip communication property. In the absence of this property, we can craft an execution where a network of validators will never reach agreement. The reason why the algorithm never terminates is due to a problem called a hidden lock.
The Tendermint consensus algorithm builds on a property called “Gossip Communication.” It is a harmless looking assumption on the surface. Being subtle, it often flies under the radar when people read, discuss, or implement this algorithm.
Despite its subtlety, the property is key for ensuring liveness of the algorithm in certain scenarios, so it is necessary, and getting it wrong can have negative consequences in implementations. For example, a network may get stuck unable to terminate, i.e., build blocks.
Recently, on two separate occasions, the question of this property came up. Why is it the way it is, why is gossip needed? I could not find any reference describing what exactly breaks when this property does not hold, so here is a stab at it.
The gossip communication property
The property as it appears in the article is as follows:
If a correct process p sends some message m at time t, all correct processes will receive m before max{t, GST } + ∆. Furthermore, if a correct process p receives some message m at time t, all correct processes will receive m before max{t, GST} + ∆.
This is not a standard assumption. A networking layer that ensures this kind of gossip property is quite powerful, compared to networking properties that other BFT consensus algorithms assume.
Implementation concerns & topology
The fact that it is a strong assumption is not the only issue. The other issue that comes up is that it is very appealing to want to implement Tendermint using direct communication between validator nodes; this would entail one-to-all communication pattern as it appears in other seminal BFT consensus algorithms like PBFT or HotStuff. Direct validator-to-validator communication comes up in conversations because it may allows some optimizations, for example signature aggregation for any kind of votes.
In general, also, direct links are easier to implement compared to a full-fledged gossip network.
To be more specific, there is distinction between two types of network topologies:
- (i) Where validators hold direct links to every other, ensuring any validator will directly send its own consensus message (specifically,
Propose,Prevote,Precommit) to every other validator, i.e., via unicast. - (ii) Where validators gossip with a random subset of the network, and they forward each other’s messages to ensure each of them sees all consensus messages circulating in the network.
Type (i) is easier to implement, debug, and maintain. But it does not ensure the Gossip Communication property. For example, a validator P0 might unicast its message m1 to all validators except to validator P1, which would never see m1. If we add a mechanism to forward messages among peers, then type (i) topology can give us the property we want.
Type (ii) is more complicated, and would implement out of the box the Gossip property we want.
Why is this assumption needed?
Briefly, there’s two parts that may break in case the gossip communication property is not ensured in an implementation of the Tendermint algorithm:
- Equivocation detection, and
- More severely, liveness
1. Equivocation
If the gossip communication property does not hold, then a validator could act in a malicious way by equivocating a consensus message and they might get away with it. For instance, a malicious validator P0 sends a Prevote for value m1 to correct validator P1 and sends a Prevote for m2 to correct validator P2. Validators P1 and P2 would consequently receive conflicting information.
To catch the equivocation, we need to ensure the latter part of the gossip property: “if a correct process p receives some message m at time t, all correct processes will receive m before max{t, GST} + ∆.” If an implementation does ensure this, then validators P1 and P2 (and other correct validators in the network) would see the equivocation.
2. Liveness
To show how liveness can break in Tendermint in the absence of the gossip communication property, we’ll build an execution that spans across multiple rounds of a single consensus height. We’ll show that we get into a situation where the algorithm cannot progress and will repeat over and over a pathological sequence of steps.
We’ll assume a small network of four validators: P0, P1, P2, and P3. We'll assume validator P0 is incorrect, so it deviates from the normal protocol. Moreover, we begin with the network being asynchronous, i.e., we are before GST; the network will eventually become synchronous.
Round 0: crafting a hidden lock
Overview. In round 0 of this execution, we’re setting the conditions for the pathological case to occur. By the end of this round, we want to create a hidden lock: A situation where a validator locks on a value m1 but does not reach decision on that value. It is hidden because no other validator gathers sufficient Prevotes to lock on the value.
The starting point of the execution we’re building here is the observation we made in describing the Type (i) network. The malicious validator P0 sends Prevote for m1 to validator P1 but never sends this message to any other validator.
In addition to validator P0 being malicious, we have one more relevant contextual element in our setup. Since the network is asynchronous, validator P3 will have all its messages delayed and will not actively participate in the beginning. Later on, P3 will take part.
In this round, we have the following sequence of actions:
- Correct validator P1 is the proposer, and they
Proposevaluem1; this validator also broadcasts to all validators aPrevotefor valuem1. - Correct validator P2 accepts this proposal and broadcasts to all validators a
Prevotefor valuem1. - Validator P3 is delayed and misses the messages above.
- Malicious validator P0 accepts proposal for
m1and sends aPrevoteform1only to validator P1, withholding this message from validator P2. - Validator P1 receives three
Prevoteform1, from validators P0, P1, and P2 respectively. Consequently, validator P1 locks on valuem1and broadcasts aPrecommitfor this value. Additionally, this validator sets these local variables:validValuetom1,validRoundto0,lockedValuetom1andlockedRoundto0. This information will be critical in round 2 (and later) of our execution. This is the hidden lock. - Validator P2 receives two
Prevoteform1(respectively from P2 and P1). This validator will not lock on any value, however, because it needs a thirdPrevoteto do so. It is missing aPrevoteform1from either malicious validator P0 or from asynchronous validator P3. For the sake of completeness, let's assume P0 equivocates by sending to P2 aPrevotefornil. Validator P2 will time-out andPrecommitfor anilvalue.
Validator P1 also times-out and is unable to reach a decision on value m1 on which it is locked. Validator P3 times-out without receiving any useful messages, and eventually transitions to the next round.
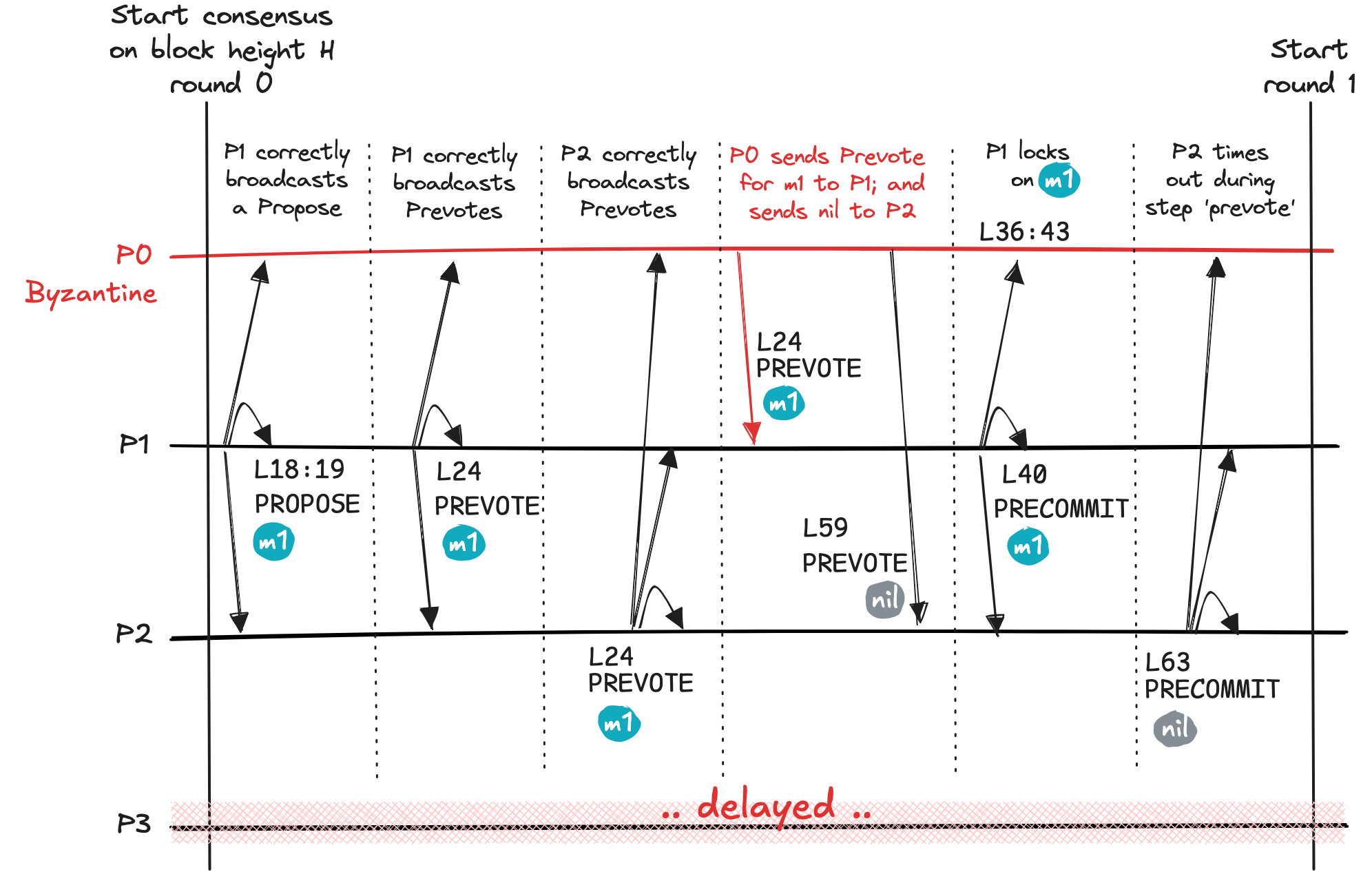
Side note. We could alternatively use a equivocation here to get to a similar situation. Namely, the malicious validator P0 would send Prevote for m1 to validator P1 and would send Prevote for m2 to validator P2. Like the description above, equivocation would similarly lead to P1 having a hidden lock on m1.
Round 1
Overview. We use this round to demonstrate the negative consequences of a hidden lock. Validator P2 is the proposer and attempts to drive the network towards a decision for a value m2. The problem is that validator P1 is locked on m1, and therefore P1 refuses to Prevote for m2. Instead, this validator sends a Prevote for nil.
The key moments in this round are the following:
- Validator P2 is the proposer and broadcasts a
Proposefor some valuem2. - Validator P0, despite being malicious, cooperates with proposer P2 by correctly broadcasting a
Prevoteform2. Despite this cooperation, the network cannot progress to a decision onm2. - Validator P1 cannot
Prevoteform2because it is locked on a different value, namely onm1. - Validator P3 is still asynchronous and is not actively participating, timing-out without receiving any message and eventually moving to the next round.
- Both P1 and P2 will time-out and send
Precommitfornil.
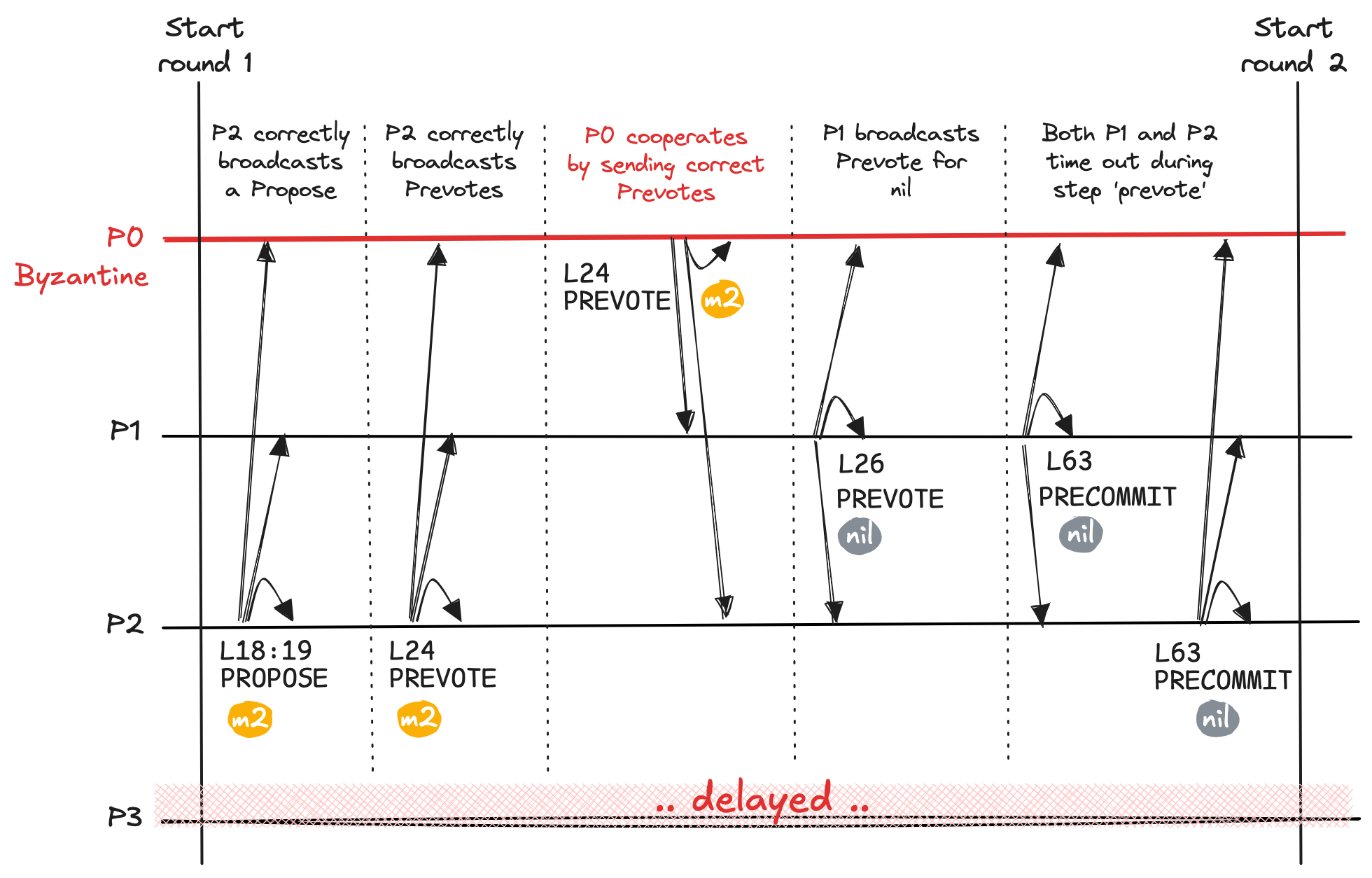
Propose for m2. The network cannot reach a decision because P1 is locked on a different value (m1) and refuses to Prevote for the proposed message.Round 2
Overview. This is a transitional round. The malicious validator P0 stops participating altogether by crashing and never recovering. The network does not progress because the asynchronous validator P3 is the proposer and the Propose message is lost. The network reaches GST at the end of round 2.
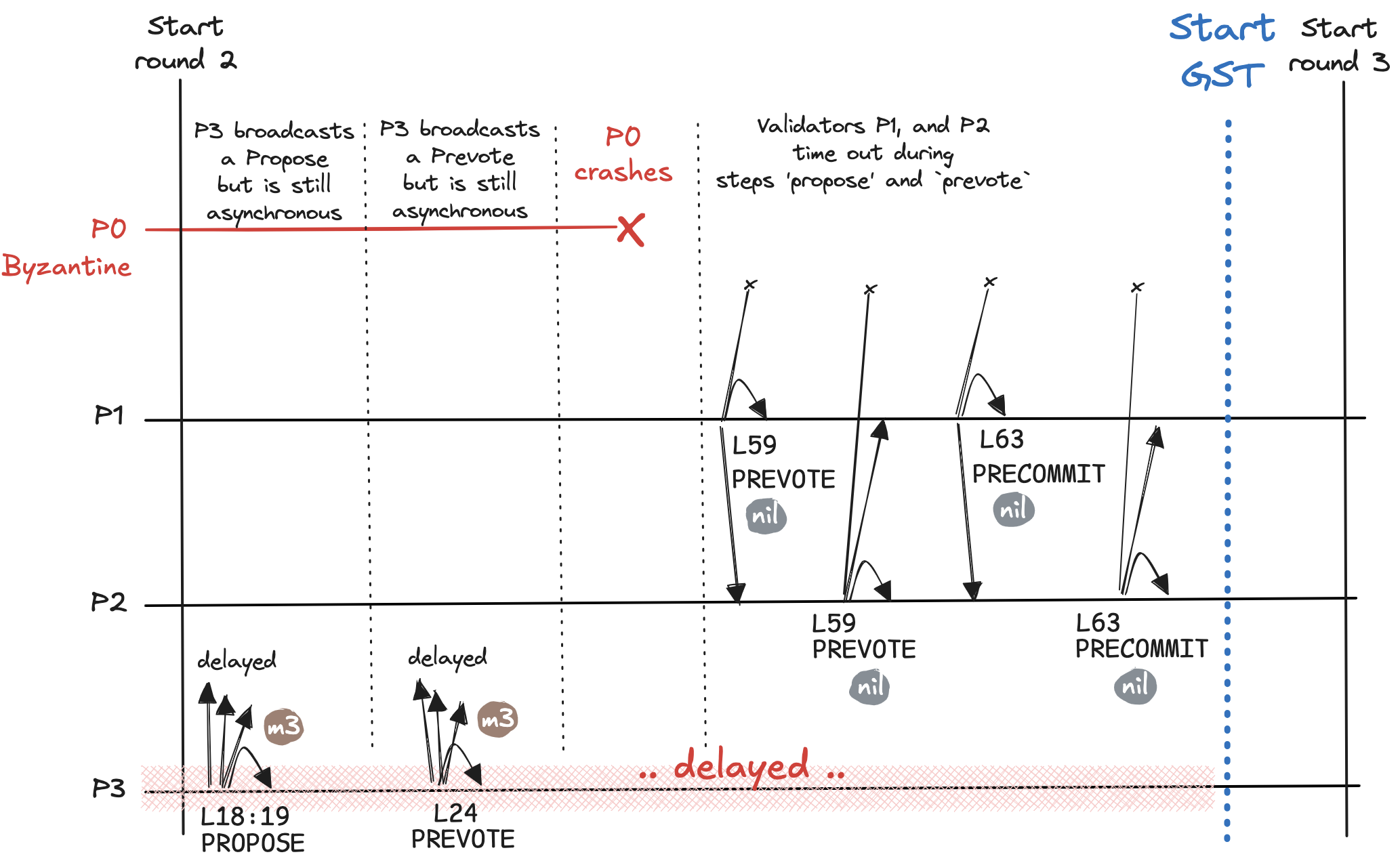
Assuming round-robin proposer selection, in round 3 we would have validator P0 as proposer. This validator crashes before round 2 ends, however. Having P0 as proposer in round 3 (and any later rounds) will look very similar to current round 2 (where the Propose message is lost). For this reason, I’ll ignore the rounds where P0 is proposer. I will assume in round 3 we have proposer P1.
Round 3, 4, and so on
Overview. The pathological case that will repeat for ever is a cycle of two patterns that repeat one after the other. Without the gossip communication property, the network will never progress to a decision.
The first patten in the cycle is illustrated in round 3.
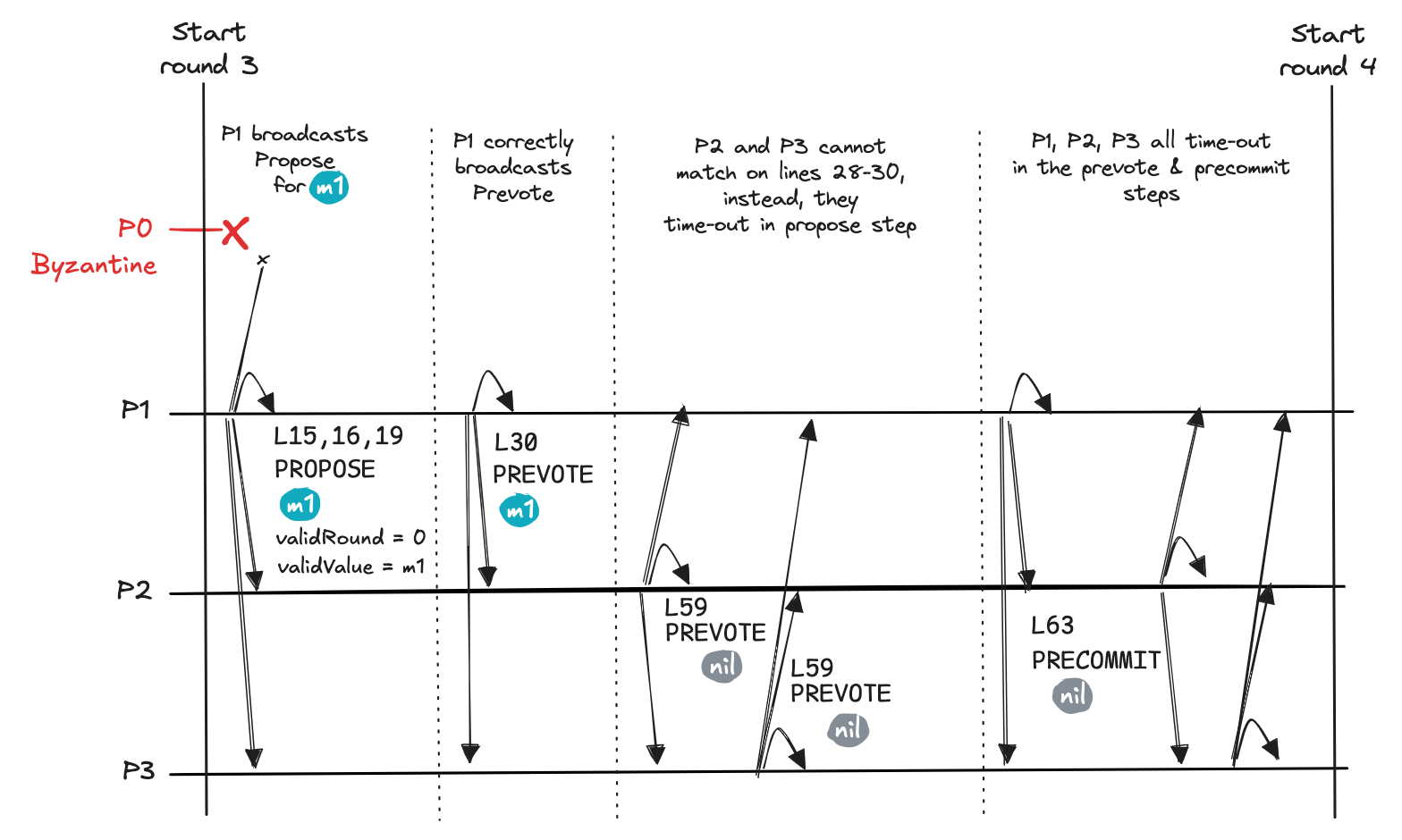
Propose message from P1.In this pattern, validator P1 is proposer. It proposes the locked value m1. The other validators P2 and P3 do not accept this value and they Prevote and Precommit on nil, so the network cannot reach a decision. The reason why validators P2 and P3 do not cooperate with P1 to decide on m1 is because these two validators cannot match on line 28 of the algorithm. They need to match on this line because the Propose message from P1 uses value 0 in the validValue field. Put differently, validRound is not -1 in the proposal, so validators P2 and P3 may only Prevote on a non-nil value (line 30) by matching on line 28.
To activate line 28, the two validators P2 and P3 need to have 2f+1 Prevote messages that are for validRound = 0 and value m1. More specifically, they are missing the Prevote of the malicious validator P0, which only sent this message to to no one else except for P1.
If validator P1 could forward to P2 and P3 the Prevote from P0 (for value m1), then these two validators could activate line 28. This is what the gossip communication property would take care of. In this execution, the property does not hold, so any round with P1 as proposer will not lead to a decision.
The second pattern is easier to explain because we’ve seen it already. It is what happened in round 1. In this pattern, one of the validators that is not locked on m1 is the proposer. Namely, either validator P2 or P3. Neither of them as a proposer manages to gather 2f+1 Prevote for their proposal on their respective value – value m3 or some other value – because validator P1 will not cooperate with them. Validator P1 can only accept a proposal for value m1. At most, the proposer can gather two non-nil Prevote, but they need 3 such votes (2f+1).
From this point on, the execution will cycle through pattern 1 (validator P1 proposer) or pattern 2 (validator P2 or P3 as proposer), being unable to terminate in either of these cases.
Reference: Ethan Buchman, Jae Kwon, Zarko Milosevic, "The latest gossip on BFT consensus," last revised 22 Nov 2019 (v3), https://arxiv.org/abs/1807.04938
Many thanks to Daniel Cason (Informal) for offering suggestions on an earlier version of this post & helping me get a deeper understanding of the hidden lock problem; Nenad Milosevic (USI; Informal) also for helping me untangle hidden locks in practical scenarios; and to @Liamzebedee and @samlafer for asking the hard question.



Comments ()